Central Limit Theorem ความลับการตลาดเพื่ออ่านค่าเฉลี่ยจากตัวอย่างข้อมูล

• Facebook
• X
• Line

สวัสดีค่ะทุกท่าน \(@^0^@)/ บทความนี้นิกจะมาแนะนำทุกท่านให้รู้จักกับทฤษฎีทางสถิติที่สำคัญมากๆ ที่ใช้คำว่าถ้าเรารู้และเข้าใจสิ่งนี้ จะทำให้เราสามารถวิเคราะห์ข้อมูลทางสถิติ (ซึ่งแน่นอนว่าสำคัญสำหรับนักการตลาดอย่างเราอยู่แล้ว) และอ่านค่าบทวิเคราะห์ทางสถิติต่างๆ ด้วยความเข้าใจที่แจ่มชัดมากยิ่งขึ้น”” และทฤษฎีที่ว่านั้นคือ Central Limit Theorem หรือหลายท่านอาจคุ้นเคยกับชื่อเล่น CTL นั่นเองค่ะ

ซึ่งสำหรับนักสถิติและ Data Analyst นั้น CLT หรือ “ทฤษฎีบทขีดจำกัดกลาง” ไม่ใช่แค่แนวคิดเชิงทฤษฎีเท่านั้น แต่ยังเป็นรากฐานสำคัญของสถิติเชิงอนุมานอีกด้วย ดังนั้นในบทความนี้ เราจะมาเจาะลึกถึงความแตกต่างเล็กๆ น้อยๆ ของ CLT ไปพร้อมๆ กัน เพื่อแสดงให้เห็นถึงตัวอย่างการใช้งานที่เป็นประโยชน์จากความเข้าใจในทฤษฎีนี้สำหรับการวิเคราะห์ข้อมูลทางธุรกิจที่ซับซ้อน==>>> บทความนี้แจก Python Code ให้ลองไปรันเล่นกันดูด้วยนะคะ^^ (∩^o^)⊃━☆ Let’s go

#1 อะไรคือ Central Limit Theorem?

คำถามแรกก่อนจะเข้าสู่การใช้งานคือ,,,, แล้ว CTL นี่คืออะไรล่ะ?
The answer is =>> Central Limit Theorem เป็นหลักการสำคัญในสถิติที่ช่วยแปลงข้อมูลที่มีลักษณะซับซ้อน หรือกระจายตัวไม่สมมาตรหรือ skewed data หรือก็คือพวกกราฟเบ้ซ้าย เบ้ขวา ที่เราเรียนกันในสิถิติ ม.ปลาย นั่นเองค่ะ ซึ่งแน่นอนว่าถ้าจะเราวิเคราะห์กราฟเหล่านี้เพิ่มเติมนอกจากรู้ว่ากราฟเบ้ เป็นสิ่งที่ค่อนข้างยาก CTL เลยจะมาช่วยเปลี่ยน skewed data

คำถามแรกก่อนจะเข้าสู่การใช้งานคือ,,,, แล้ว CTL นี่คืออะไรล่ะ?
The answer is =>> Central Limit Theorem เป็นหลักการสำคัญในสถิติที่ช่วยแปลงข้อมูลที่มีลักษณะซับซ้อน หรือกระจายตัวไม่สมมาตรหรือ skewed data หรือก็คือพวกกราฟเบ้ซ้าย เบ้ขวา ที่เราเรียนกันในสิถิติ ม.ปลาย นั่นเองค่ะ ซึ่งแน่นอนว่าถ้าจะเราวิเคราะห์กราฟเหล่านี้เพิ่มเติมนอกจากรู้ว่ากราฟเบ้ เป็นสิ่งที่ค่อนข้างยาก CTL เลยจะมาช่วยเปลี่ยน skewed data เหล่านี้ให้กลายเป็นข้อมูลที่สามารถวิเคราะห์ได้ง่ายขึ้น

โดย CLT บอกเราว่าหากเราทำการสุ่มตัวอย่างจากประชากรใดซ้ำๆ ขนาดของกลุ่มตัวอย่างมีขนาดใหญ่พอ การแจกแจงค่าเฉลี่ยของตัวอย่างเหล่านั้นจะมีลักษณะใกล้เคียงกับการแจกแจงแบบปกติ (Normal Distribution) แม้ว่าข้อมูลประชากรเดิมจะไม่ได้มีลักษณะแบบปกติก็ตาม

ดังนั้น CLT จึงมีบทบาทสำคัญในงานวิเคราะห์ข้อมูลและการตัดสินใจเชิงธุรกิจ โดยเฉพาะในบริบทที่เกี่ยวข้องกับการทดสอบสมมติฐาน การปรับปรุงแคมเปญการตลาด และการประเมินความเสี่ยงทางการเงิน

#2 หลักการพื้นฐานของ Central Limit Theorem

2.1 การแจกแจงของค่าเฉลี่ยตัวอย่างมีแนวโน้มเข้าใกล้ Normal Distribution

หากเราทำการสุ่มตัวอย่าง (sampling) จากประชากรใดๆ ที่มีการแจกแจงรูปแบบใดๆ ก็ตาม (อาจจะเป็น Skewed, Bimodal หรืออื่น ๆ) และคำนวณค่าเฉลี่ยของแต่ละตัวอย่าง เมื่อจำนวนตัวอย่าง (sample size: n) มีขนาดใหญ่เพียงพอ การแจกแจงของค่าเฉลี่ยตัวอย่างจะเข้าใกล้การแจกแจงแบบปกติ (Normal Distribution) แม้ว่าข้อมูลประชากรเดิมจะไม่ได้มีลักษณะปกติก็ตาม (ซึ่งการแจกแจงแบบปกติที่ว่าคือกราฟรูประฆังคว่ำแบบสมมาตร ที่เราคุ้นเคยกันนั่นเองค่ะ)

โดยข้อมูลที่เรามักพบเจอและจะต้องใช้ CTL ปรับปรุงก็ยกตัวอย่างเช่น ข้อมูลประชากรที่กระจายตัวในลักษณะเบ้ ได้แก่ รายได้ของประชากรที่มีคนรวยน้อยและคนจนเยอะ เมื่อสุ่มตัวอย่างและคำนวณค่าเฉลี่ยของแต่ละกลุ่มตัวอย่าง ค่าเฉลี่ยเหล่านั้นจะเริ่มแสดงลักษณะของการแจกแจงแบบปกติเมื่อ จำนวนตัวอย่าง: n มีขนาดใหญ่ขึ้นมากพอ

2.2 ค่าเฉลี่ยของการแจกแจงตัวอย่างเท่ากับค่าเฉลี่ยของประชากร

และค่าเฉลี่ย (μ) ของการแจกแจงค่าเฉลี่ยกลุ่มตัวอย่าง จะเท่ากับค่าเฉลี่ยของประชากรต้นทาง ซึ่งหมายความว่าการสุ่มตัวอย่างที่เพียงพอ และเหมาะสมจะช่วยให้เราสามารถประมาณค่าค่าเฉลี่ยประชากรได้อย่างแม่นยำตามสมการ

เพื่อให้เห็นภาพชัดนะคะ ยกตัวอย่างเช่น หากประชากรทั้งหมดมีค่าเฉลี่ยการใช้งาน TikTok ต่อวันเป็น 2.5 ชั่วโมง เมื่อเราสุ่มตัวอย่างแบบสุ่ม (random sampling) ซ้ำๆ และคำนวณค่าเฉลี่ยตัวอย่าง จะพบว่าค่าเฉลี่ยเหล่านั้นมีแนวโน้มเข้าใกล้ 2.5 ชั่วโมง

ซึ่งทำให้ค่าความแปรปรวนของการแจกแจงค่าเฉลี่ยตัวอย่าง (Standard Error) ลดลงเมื่อขนาดตัวอย่าง: n เพิ่มขึ้น ซึ่งแสดงว่าค่าเฉลี่ยของตัวอย่างจะ “แม่นยำ” มากขึ้นเมื่อเรามีตัวอย่างใหญ่ขึ้น (พูดง่ายๆ ค่ะว่า ก็แปรปรวนน้อยลง Error น้อยลง เลยแม่นยำขึ้น) ตามสมการ

เมื่อ σ คือส่วนเบี่ยงเบนมาตรฐานของประชากร และ n คือขนาดตัวอย่าง ค่ะ ซึ่งตัวอย่างที่มีขนาดใหญ่ช่วยลดความไม่แน่นอนของค่าเฉลี่ยตัวอย่าง และทำให้เราได้ค่าที่ใกล้เคียงกับประชากรมากขึ้น ดังนั้น การเพิ่มขนาดตัวอย่างช่วยให้การประมาณค่าประชากรมีความแม่นยำมากขึ้น

2.3 สรุปการใช้ CTL

• การแจกแจงค่าเฉลี่ยตัวอย่างเข้าใกล้ Normal Distribution เมื่อ n เพิ่มขึ้น
• ค่าเฉลี่ยของค่าเฉลี่ยตัวอย่างเท่ากับค่าเฉลี่ยประชากร
• ความแปรปรวนของค่าเฉลี่ยตัวอย่าง (Standard Error) ลดลงเมื่อ n เพิ่มขึ้น

2.4 ความสำคัญของ CLT ในการวิเคราะห์ข้อมูล:

• ทำให้การวิเคราะห์ข้อมูลที่มีการกระจายซับซ้อนง่ายและแม่นยำขึ้นการแจกแจงค่าเฉลี่ยตัวอย่างเข้าใกล้ Normal Distribution เมื่อ n เพิ่มขึ้น
• ค่าเฉลี่ยของค่าเฉลี่ยตัวอย่างเท่ากับค่าเฉลี่ยประชากร
• ความแปรปรวนของค่าเฉลี่ยตัวอย่าง (Standard Error) ลดลงเมื่อ n เพิ่มขึ้น

ซึ่งเพื่อนๆ ลองดูภาพด้านล่างนี้นะคะ จะเห็นว่าที่กลุ่มตัวอย่าง n มีจำนวนเท่ากับ 5 จะได้กราฟเป็นแบบเบ้ (Skewed) ตามรูปขวาบน ในขณะที่ยิ่งเราเพิ่ม n เป็น 30 หรือ 100 กราฟก็จะยิ่งกลายเป็นรูประฆังคว่ำหรือเข้าสู้ Normal Distribution มากขึ้นตามลำดับค่ะ

ป.ล. สำหรับเพื่อนๆ ที่อยากรัน Python Code สามารถใช้: CTL_colab ได้เลยค่ะ^^

2.5 ความสำคัญของ CLT ในการวิเคราะห์ข้อมูล:

• ทำให้การวิเคราะห์ข้อมูลที่มีการกระจายซับซ้อนง่ายและแม่นยำขึ้น
• ช่วยในการประมาณค่าคุณสมบัติของประชากรโดยไม่ต้องใช้ประชากรทั้งหมด
• เป็นพื้นฐานสำหรับการทดสอบสมมติฐานและการวิเคราะห์ข้อมูลในสถานการณ์จริง
• ช่วยในการประมาณค่าคุณสมบัติของประชากรโดยไม่ต้องใช้ประชากรทั้งหมด
• เป็นพื้นฐานสำหรับการทดสอบสมมติฐานและการวิเคราะห์ข้อมูลในสถานการณ์จริง

#3 ตัวอย่างการใช้งานในเชิง Marketing/ Marketing Advertisement

เราสามารถให้ Central Limit Theorem ในการทดสอบสมมติฐาน (Hypothesis Testing): เพื่อให้สามารถใช้ค่าเฉลี่ยตัวอย่างในการทดสอบสมมติฐานเกี่ยวกับประชากร เช่น การเปรียบเทียบผลลัพธ์จากแคมเปญการตลาดสองรูปแบบ หรือให้ในการประเมินผลแคมเปญการตลาด (Marketing Campaign Optimization): เพื่อช่วยวิเคราะห์ผลตอบแทนจากการลงทุน (ROI) ของแคมเปญโดยประเมินจากตัวอย่างลูกค้า หรือแม้แต่ใช้ในการการคาดการณ์ความเสี่ยงทางการเงิน (Risk Prediction) ซึ่ง CTL ใช้ช่วยในการประเมินความผันผวนของตลาดหรือความน่าจะเป็นของการขาดทุนในสถานการณ์ต่างๆ

โดยนิกขอยกตัวอย่างการใช้งานแบบ Case by case ดังนี้ค่ะ (☞ﾟヮﾟ)☞

3.1 การทดสอบประสิทธิภาพของโฆษณา (A/B Testing):

• กรณีบริษัทโฆษณาต้องการเปรียบเทียบผลลัพธ์ของโฆษณาสองเวอร์ชัน (A และ B) ที่เผยแพร่บนแพลตฟอร์มโซเชียลมีเดีย
• โดยใช้ CLT บริษัทสามารถสุ่มเลือกตัวอย่างกลุ่มลูกค้าที่คลิกโฆษณา A และ B มาเปรียบเทียบค่าเฉลี่ยของ Conversion Rate
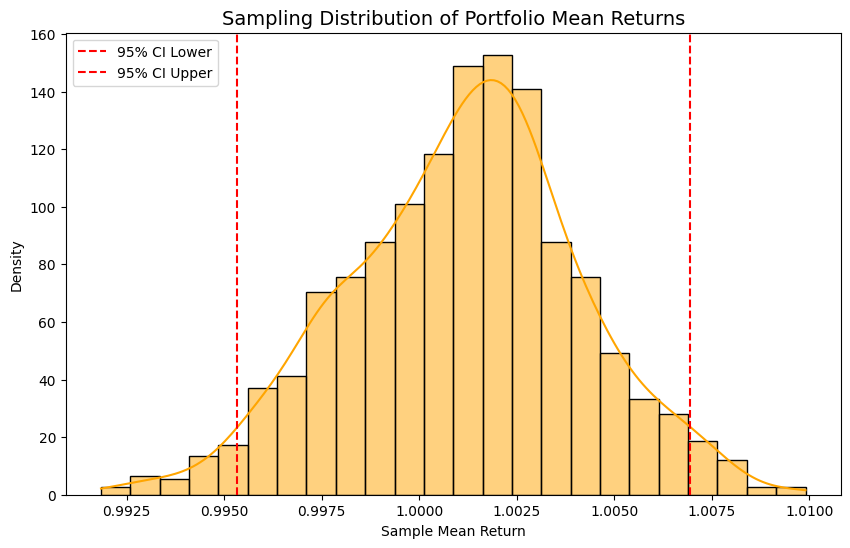
• หากข้อมูลประชากรของ Conversion Rate มีความเบ้หรือไม่สมมาตร CLT จะช่วยให้ค่าเฉลี่ยของตัวอย่างเข้าใกล้การแจกแจงแบบปกติและทำให้การวิเคราะห์เชิงสถิติแม่นยำขึ้น ตามภาพด้านล่างค่ะ

3.2 การปรับปรุงการตั้งเป้าหมายกลุ่มลูกค้า:

• นักการตลาดสามารถใช้ข้อมูลตัวอย่างจากพฤติกรรมของลูกค้ากลุ่มหนึ่ง เช่น การซื้อสินค้าหรือการคลิกโฆษณา เพื่อประมาณการแนวโน้มพฤติกรรมของลูกค้าทั้งหมด
• ด้วย CLT การวิเคราะห์ข้อมูลตัวอย่างจะมีความน่าเชื่อถือและสามารถนำไปปรับปรุงการตั้งเป้าหมายโฆษณาให้เหมาะสมกับกลุ่มลูกค้าเป้าหมายได้

3.3 การคาดการณ์ยอดขายสินค้าใหม่:

• หากบริษัทเปิดตัวสินค้าใหม่และเก็บข้อมูลยอดขายจากสาขาบางแห่งในช่วงเริ่มต้น
• CLT สามารถใช้ในการคาดการณ์ยอดขายรวมของสินค้าทุกสาขา โดยอิงจากค่าเฉลี่ยของตัวอย่างข้อมูลยอดขายเริ่มต้นนั้น

\(@^0^@)/

Last but not Least..

Key takeaway: Central Limit Theorem เป็นเครื่องมือที่เปลี่ยน “ความไม่แน่นอน” ให้กลายเป็น “ความเข้าใจที่สามารถนำไปปฏิบัติได้” ซึ่งนักสถิติและผู้ตัดสินใจเชิงกลยุทธ์การตลาดควรเรียนรู้/ทำความเข้าใจ และนำ CLT ไปปรับใช้ เพื่อสร้างความได้เปรียบในโลกที่ขับเคลื่อนด้วยข้อมูลอย่างยุคปัจจุบัน ซึ่งความเข้าใจนี้เองค่ะ จะช่วยเพิ่มผลตอบแทนทางการตลาด ลดความเสี่ยงในการสูญเงินลงทุนอย่างเปล่าประโยชน์ ตามหลักการสร้างกลยุทธ์แบบ Data Driven ได้^^
และสำหรับท่านใดที่ต้องการรัน Python code สามารถเข้าไปดูโค้ดทั้งหมดในบทความนี้ได้ที่ ULR: CTL_Python_code_by_nick_panaya

หรือหากอยากศึกษาเพิ่มเติม แนะนำที่ =>>

• Facebook
• X
• Line